Numerical aperture (abbreviated as ‘NA’) is an important consideration when trying to distinguish details in a sample observed under a microscope. NA is a unitless number related to the angle of light collected by the lens. The refractive index of the medium is also taken into account when calculating the numerical aperture (NA) (see below). By matching the refractive index of the slide or cell culture container to the immersion medium, more details of the sample can be resolved. The way light behaves when traveling from one medium to another is also related to the numerical aperture (NA) (called “refraction”). This article also provides a brief history of refraction and how this concept can be a limiting factor in achieving high NA.

Microscope objective
The objective lenses on a microscope have a variety of different information and numbers engraved on the barrel. In addition to magnification and optical correction, there is another set of numbers without units. This is the numerical aperture (or ‘NA’) on the objective lens (see Figure 1).
The NA of the objective is relatively important and related to image resolution. Simply put, resolution refers to the ability of an objective lens to distinguish details in a sample. Without a corresponding high numerical aperture (NA), a high-magnification objective lens cannot resolve the details of the sample.
Simply put, the numerical aperture (NA) of a microscope objective is the lens’s ability to collect light at a fixed distance from the object being observed. As light passes through the sample, it enters the objective lens in an inverted cone. But some of the light in the sample will be refracted (and reflected), which in turn creates an image that has higher resolution and contains more detail than an objective with a lower NA.

Aperture angle
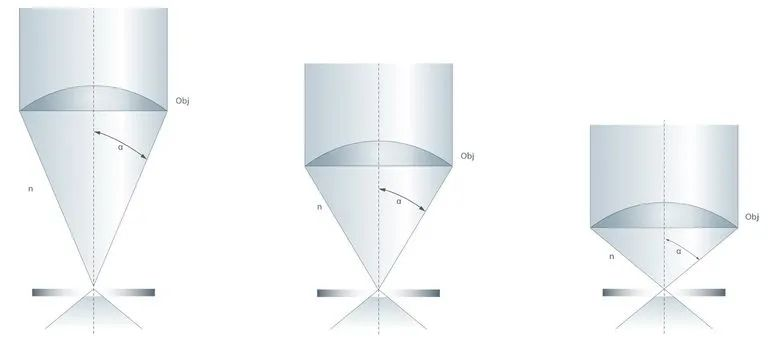
The maximum radial angle of the light cone angle collected by the front lens of the objective is also called the ‘aperture angle’ (see Figure 1). In addition to increasing NA, image brightness is also proportional to aperture angle. The aperture angle varies with the focal length of the objective and is related to the maximum angle at which the imaging rays emitted from the specimen are captured by the objective front lens when the specimen is focused.
Aperture angle is inversely proportional to objective focal length. As the focal length decreases, the amount of light that can be collected by the front lens of the objective increases. In other words, if the objective lens is very close to the sample, then the objective lens can collect more oblique light. It should be said that the aperture angle is usually determined by the optical elements within the objective lens, and each objective lens has an optimal focal length. As an analogy, imagine this: if you are standing in front of a door with a keyhole looking into another room, then when you are far away you can only see a little light from the room and very little thing. If you put your eye close to the keyhole, you will see more detail and light in the room because you theoretically increase the aperture angle of your eye.
The brightness and image detail (resolution) of the image collected and formed by the objective lens are related to the aperture angle. Light from the specimen passes continuously through the air between the coverslip and the objective front lens or through the immersion medium.
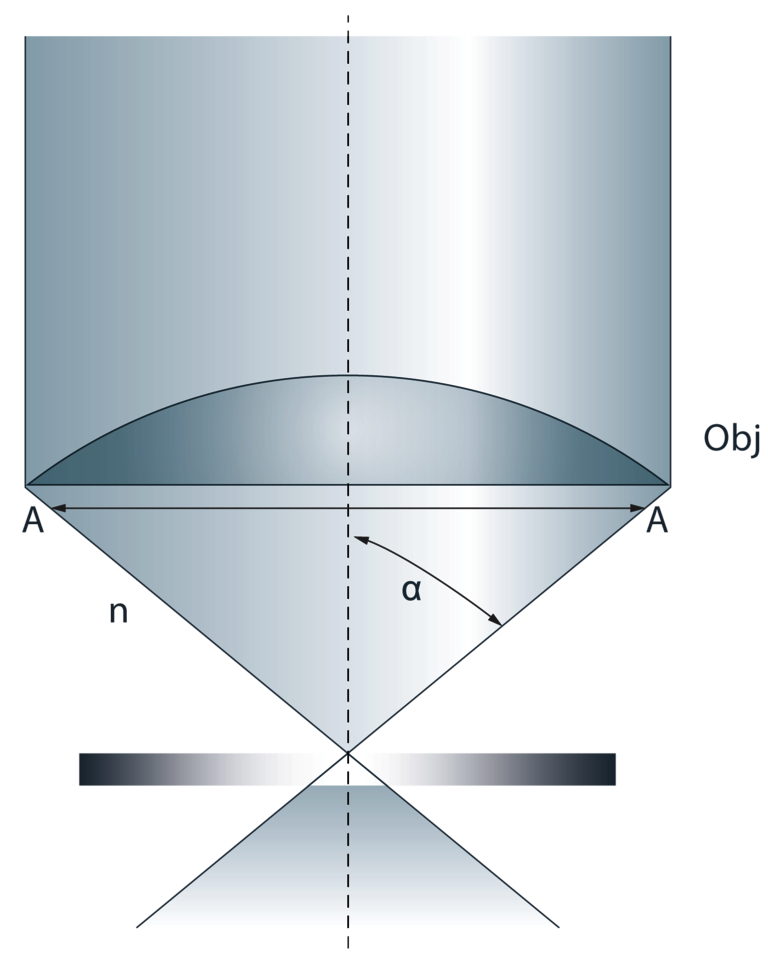
Calculation of NA
The numerical aperture can be expressed and determined using the following formula:
Numerical aperture (NA) = n • sin (α)
In the above formula, ‘n’ is the refractive index of the medium between the cover glass and the objective front lens (e.g. air, water or oil). The ‘α’ symbol relates to the half-angle of the light cone angle and that can be collected through the lens (i.e. the aperture angle; see Figure 2).
The refractive index of air is about 1.0, while the refractive index of water is 1.3, and some immersion oils used in optical microscopy can have a refractive index as high as 1.52.
Refraction
To fully understand numerical aperture (NA), it helps to first understand refraction. In optics and microscopy, refraction is the change in the direction of light waves as they travel through and from a sample, due to changes in the medium through which the light travels (such as air, glass, water, or oil). The formula in ‘Snell’s Law’ describes refraction very well. Willebrord Snellius (1580-1626) was a Dutch mathematician and astronomer. He established a new method of calculating the radius of the Earth and became famous for his mathematical description of refraction. But he was not the first to describe the phenomenon of refraction mathematically. To be more precise, he simply “rediscovered” the description of this phenomenon by the Persian mathematical physicist Ibn Sahl. In a manuscript written in 1984, Ibn Sahl described how curved lenses and mirrors bend and focus light.
Snell’s law states that the ratio of the angles of incident light and refracted light is equal to the reciprocal of the ratio of the refractive indices through which the light passes.
Simply put, when light travels from one medium to another, its speed changes, such as when light travels from air to water, the speed of light slows down. Additionally, when light enters a medium at an angle other than 90°, changes in its speed cause a change in direction. It is important to note that the frequency of the light will not change, but the wavelength will be determined by the properties of the medium.
Theoretically, the maximum aperture angle of the light cone collected by the front lens of the objective lens is 180°, and the α value is 90°. Since the sine of 90 degrees has a value of 1, an objective capable of collecting 180° of synthetic light from a sample in an air medium also has a theoretical numerical aperture (NA) value of 1. Clearly, the refractive index is the limiting factor in achieving the highest numerical aperture (NA) of an objective lens. Therefore, high numerical aperture (NA) objectives use an immersion medium instead of air, such as oil or water. In reality, it is impossible to achieve a numerical aperture (NA) value of 1 when there is air between the specimen and the objective front lens, so the highest numerical aperture (NA) value for a “dry lens” (i.e., a non-immersion objective) is closer to 0.95. This is because most lenses cannot collect 180° of light from the sample, and the widest angle is about 144°. The sine of 144° is 0.95 and the refractive index of air is 1.0, so the theoretical maximum numerical aperture (NA) is close to 0.95.
High-magnification objectives paired with lower numerical aperture (NA) will ultimately result in lower resolution. Many microscope companies try to increase the numerical aperture (NA) of their objective lenses as much as possible. So if you are considering buying new lenses for your microscope, always consider how to get the highest NA objective within your budget.