A lens is an optical component made of transparent material with a surface that is part of a spherical surface. Lenses are composed of several lens pieces, including plastic lenses and glass lenses, with glass lenses being more expensive than plastic ones. Common lens constructions used in cameras include 1P, 2P, 1G1P, 1G2P, 2G2P, 4G, etc. The more lenses there are, the higher the cost. Therefore, a high-quality camera should use glass lenses, which provide better imaging results compared to plastic lenses and play a crucial role in astronomy, military, transportation, medicine, art, and other fields.
I. What is a Lens

Lenses can be widely used in security, eyewear, digital cameras, lasers, optical instruments, and many other fields. With the continuous development of the market, lens technology is becoming increasingly widespread.
A lens is made according to the law of light refraction. It is an optical component made of transparent materials such as glass or crystal. Lenses are refractive mirrors, with their refractive surface being two spherical surfaces (part of a spherical surface), or one spherical surface (part of a spherical surface) and one flat surface, forming both real and virtual images.
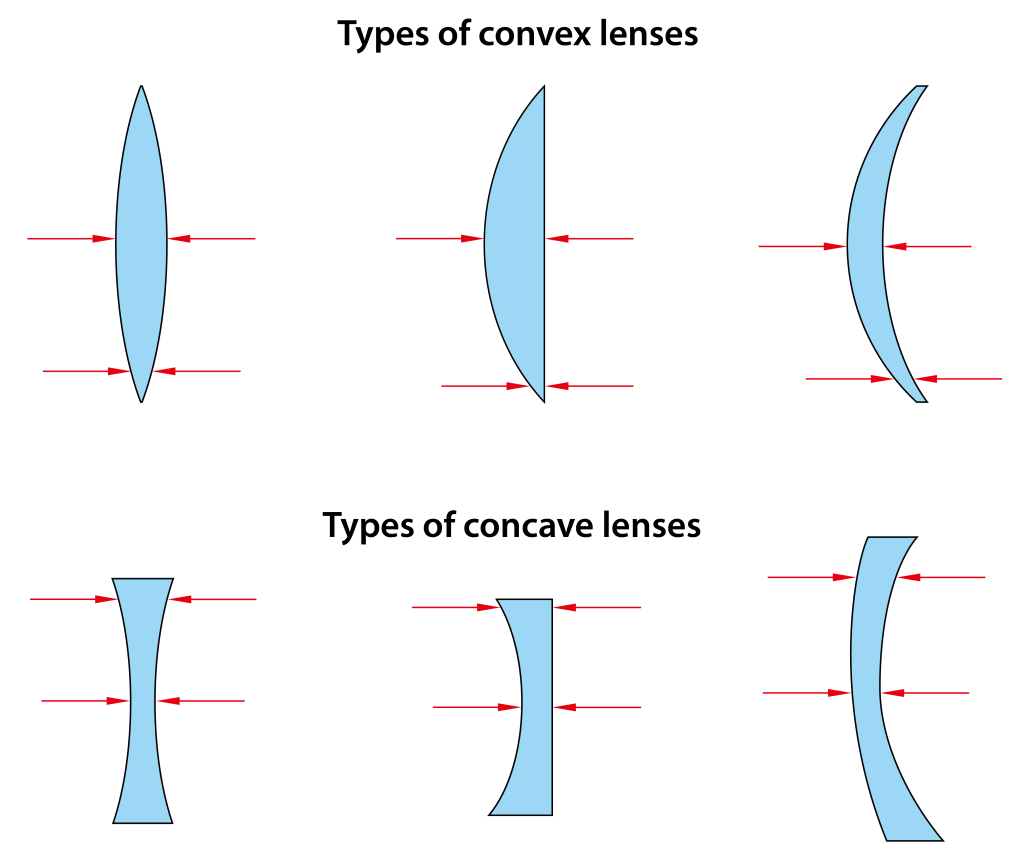
Convex Lens: Thicker in the middle and thinner at the edges, including biconvex, plano-convex, and convex-concave types.
Concave Lens: Thinner in the middle and thicker at the edges, including biconcave, plano-concave, and concave-convex types.
A thin lens refers to a lens where the thickness of the central part compared to the curvature radius of its two sides is significantly small. Initially, cameras only had a single convex lens, hence called “single lens.” With technological advancements, modern lenses consist of multiple convex and concave lenses with different forms and functions, forming a converging lens known as a “compound lens.” The concave lens in a compound lens corrects various aberrations.
Optical glass, known for its high transparency, purity, colorlessness, uniform texture, and good refractive ability, is the main material for lens production. Different types of optical glass exist due to variations in chemical composition and refractive index:
Flint Glass: Contains lead oxide to increase the refractive index (1.8804).
Crown Glass: Contains sodium oxide and calcium oxide to decrease the refractive index (barium crown glass has a refractive index of 1.7055).
Lanthanum Crown Glass: A newly discovered type with a high refractive index and low dispersion, providing excellent conditions for creating large-diameter high-end lenses.
Lenses are the most basic optical components in constructing microscope optical systems, with components like objective lenses, eyepieces, and condenser lenses composed of single and multiple lenses. Based on their shapes, lenses can be divided into convex (positive) and concave (negative) lenses.
When a bundle of light rays parallel to the principal axis passes through a convex lens and converges at a point, this point is called the “focus,” and the plane passing through the focus and perpendicular to the axis is called the “focal plane.” There are two focal points: the object-side focal point in object space is called the “object-side focal point” and its corresponding focal plane is called the “object-side focal plane”; conversely, the image-side focal point in image space is called the “image-side focal point,” and its focal plane is the “image-side focal plane.”
Light passing through a concave lens forms an erect virtual image, while a convex lens forms an inverted real image. Real images can be displayed on a screen, but virtual images cannot.
II. Classification of Lenses
1. Convex Lens
A convex lens is thicker in the center and thinner at the edges. It has the function of converging light rays, hence also known as a “converging lens” or “positive lens” (used for farsightedness and presbyopia). Convex lenses can be classified into:
- a. Biconvex Lens: Both sides are convex.
- b. Plano-Convex Lens: One side is convex, and the other side is flat.
- c. Convex-Concave Lens: One side is convex, and the other side is concave.
The imaging rule of convex lenses states that when an object is placed beyond the focus, an inverted image is formed on the opposite side of the convex lens.
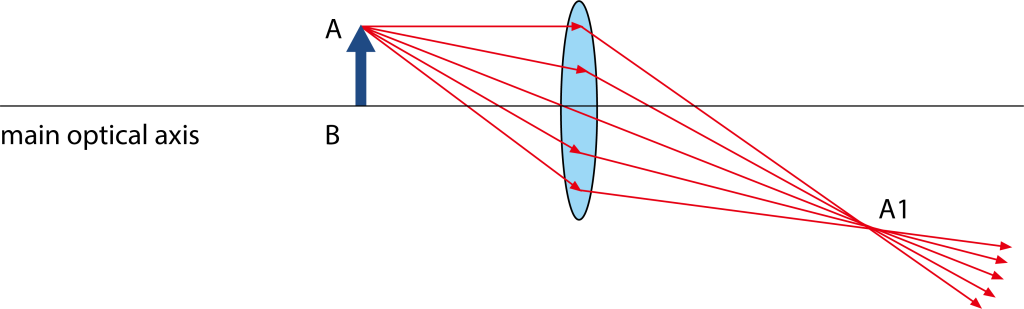
Real images formed by convex lenses can be magnified, reduced, or of the same size. The smaller the object distance, the larger the image distance, and the larger the real image. When the object is placed within the focus, a magnified erect virtual image is formed on the same side of the convex lens. The smaller the object distance, the smaller the image distance, and the smaller the virtual image. In optics, an image formed by actual light rays converging is called a real image and can be displayed on a screen; conversely, an image formed by perceived light rays is called a virtual image and can only be sensed by the eye. Experienced physics teachers often distinguish between real and virtual images by stating, “Real images are inverted, while virtual images are erect,” in relation to the original object.
When parallel rays (like sunlight) are directed parallel to the principal axis (the line connecting the centers of curvature of the two spherical surfaces of the convex lens) into a convex lens, after undergoing two refractions on the two sides of the lens, they converge to a point on the axis called the focal point (denoted as F), which is the focus of the convex lens. A convex lens has a real focus on both sides of the lens. For a thin lens, the distance from these two foci to the lens center is approximately equal. The focal length (denoted as f) of a convex lens is the distance from the focus to the lens center. The smaller the radius of curvature of the convex lens surface, the shorter the focal length (denoted as f, in English as focal length).
Convex lenses are used in magnifying glasses, reading glasses for presbyopia and farsightedness, cameras, projectors, microscopes, and telescopes.
Principal Axis: The straight line passing through the centers C1 and C2 of the spherical surfaces of the convex lens is called the principal axis.
Optical Center: Point O at the center of the convex lens is the optical center.
Focus: Parallel light rays to the principal axis converge at a point F on the principal axis after passing through the convex lens. This point is the focus of the convex lens.
Focal Length: The distance from focus F to the optical center O of the convex lens is called the focal length, denoted as f.
Object Distance: The distance from the object to the optical center of the convex lens is called the object distance, denoted as u.
Image Distance: The distance from the image formed by the convex lens to the optical center of the convex lens is called the image distance, denoted as v.
Formula: 1/u (object distance) + 1/v (image distance) = 1/f (lens focal length)
(Regarding the positive/negative signs: The object distance u is always positive. The sign of the image distance v is determined by whether the image is real or virtual; it is positive for real images and negative for virtual images. The focal length f of a convex lens is positive, while for a concave lens, it is negative.)
2. Concave Lens
A concave lens, also known as a negative spherical lens, has a thin center and thick edges, forming a concave shape, hence also called a concave lens.
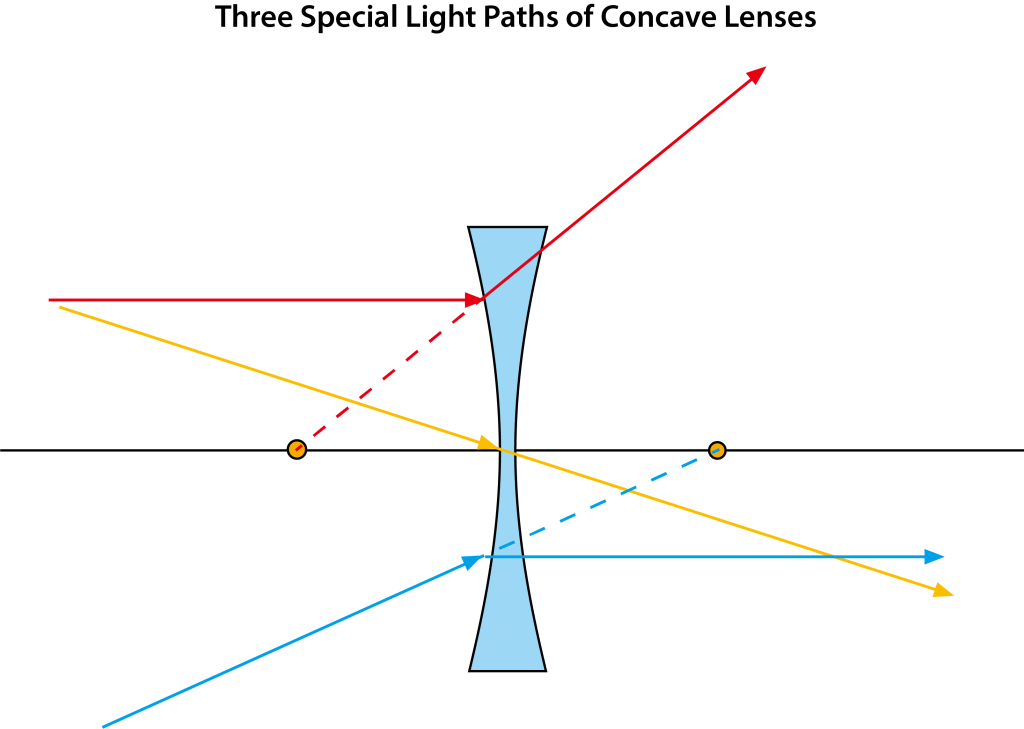
Concave lenses have a diverging effect on light. When parallel light rays pass through a concave spherical lens and diverge, they form diverging light rays, incapable of forming a real focal point. Extending along the reverse direction of the diverging light rays, they converge on the same side as the light source at point F, forming a virtual focal point.
The geometric drawing for imaging with concave lenses follows the same principles as convex lenses. Lines are drawn from the top of the object: one parallel to the principal axis, after passing through the concave lens, diverges into diverging light rays and returns these refracted light rays to the main focal point; the other line passes through the optical center of the lens, and these two lines intersect at a point, forming the image of the object.
The image formed by a concave lens is always smaller and erect than the object. Concave lenses are mainly used for correcting myopia.
Concave lenses have a diverging effect on light, hence also called “diverging lenses” or “negative lenses” (used for myopic glasses). These lenses can be classified as:
- a. Biconcave Lens: Both sides are concave.
- b. Plano-Concave Lens: One side is concave, and the other side is flat.
- c. Concave-Convex Lens: One side is concave, and the other side is convex.
The line connecting the centers of curvature of the two curved surfaces is called the principal axis, with the point O at the center being the optical center of the concave lens. Light rays passing through the optical center do not refract regardless of their direction. A beam of light parallel to the principal axis refracted through the concave lens diverges in all directions, and the extension of these diverging rays converges at a point F on the same side as the light source. This refracted light appears as if emanating from point F, which is the virtual focus point. There is one such focus point on each side of the concave lens. Concave lenses are also known as diverging lenses. The focal length of a concave lens refers to the distance from the focus to the center of the lens. The larger the radius of curvature of the lens surface, the longer the focal length. For a thin lens, the focal lengths on both sides are equal.
The image formed by a concave lens is always smaller than the object.
III. Functions of Lenses
Due to their strong converging ability, lenses are used for illumination, providing not only bright but also clear road surfaces.
As light dispersion is minimal, the light range of lenses is longer and clearer compared to ordinary halogen lamps. This allows you to see distant objects clearly and avoid crossing intersections or missing targets.
Lens-type headlights have uniform brightness and strong penetration compared to traditional headlights, providing strong penetration in rainy or foggy weather. This ensures that approaching vehicles receive light signals promptly, preventing accidents.
The lifespan of HID bulbs inside lenses is 8 to 10 times longer than that of ordinary bulbs, reducing the unnecessary trouble of frequent bulb replacements.
Xenon lamps inside lenses do not require additional power supply systems since true HID gas discharge lamps require a voltage stabilizer, 12V voltage, followed by converting the voltage to normal levels to supply the xenon bulb with light continuously. This helps save energy.
Similar to point 5, since the lens bulb boosts from stabilizer to 23,000V, stimulating xenon to achieve high brightness at startup, it can maintain brightness for 3 to 4 seconds even in case of power failure. This allows you to prepare for parking in emergencies, preventing disasters. Traditional halogen lamps cannot do this.
When encountering large trucks or vehicles with their lights on, you can notify them by using high beams if other methods are ineffective.
IV. Three differences between lenses
- Structural Differences
Convex lenses are composed of two transparent mirror bodies with spherical surfaces ground on both sides, thinning at both ends and thicker in the middle.
Concave lenses are composed of two mirror bodies with concave spherical surfaces ground on both sides, thicker at both ends, and thinner in the middle.
- Different Effects on Light
Convex lenses mainly converge light rays, but they also have a diverging effect when the object distance is less than the focal length.
Concave lenses mainly diverge light rays.
- Different Imaging Properties
Convex lenses form refracted images.
Concave lenses form “erect virtual images after light passes through them, while convex lenses form inverted real images. Real images can be displayed on a screen, while virtual images cannot.”
Overall, lenses are indispensable components in various optical applications, offering unique functionalities based on their types and configurations.