Airy Disk, Abbe Diffraction Limit, and Rayleigh Criterion
In microscopy, the term ‘resolution’ is used to describe the ability of a microscope to distinguish fine details. In other words, this is the smallest distance between two physical points within the sample that can be distinguished by an observer or a microscope camera.
The resolution of a microscope is inherently related to the numerical aperture (NA) of the optics and the wavelength of light used to observe the sample specimen. Furthermore, we have to take into account the diffraction limit first proposed by Ernst Abbe in 1873.
Resolution and Numerical Aperture
The numerical aperture (NA) is related to the refractive index (n) of the medium through which light passes and the aperture angle (α) of a given objective lens (NA=n×sinα).
The resolution of a microscope depends not only on the NA of the objective but also on the NA of the entire system, taking into account the NA of the microscope condenser.
In a microscope system, all optical components are properly aligned, have relatively high NA values, and work in harmony to resolve more image detail.
Resolution is also related to the wavelength of light used to image the specimen; the shorter the wavelength, the more detail can be resolved, and the longer the wavelength, the less detail can be resolved.
There are three mathematical concepts to consider when dealing with resolution: ‘Abbe’s Diffraction Limit‘, ‘Airy Disk‘, and ‘Rayleigh Criterion‘.
Resolution and Contrast Limits: Airy Disk
Diffraction occurs when light passes through an aperture of any size (every lens has a finite aperture). The resulting diffraction pattern (a bright area in the center surrounded by a series of concentric rings of decreasing brightness) is known as the Airy disk.
The diameter of this pattern is related to the wavelength of the illuminating light (λ) and the size of the circular aperture, which is important because the Airy disk is the smallest point on which the beam can be focused.
As the Airy disk patterns resulting from focusing on different details on the subject gather, they begin to overlap. When overlapping patterns have a large enough effect on reducing contrast, they eventually become indistinguishable from each other.
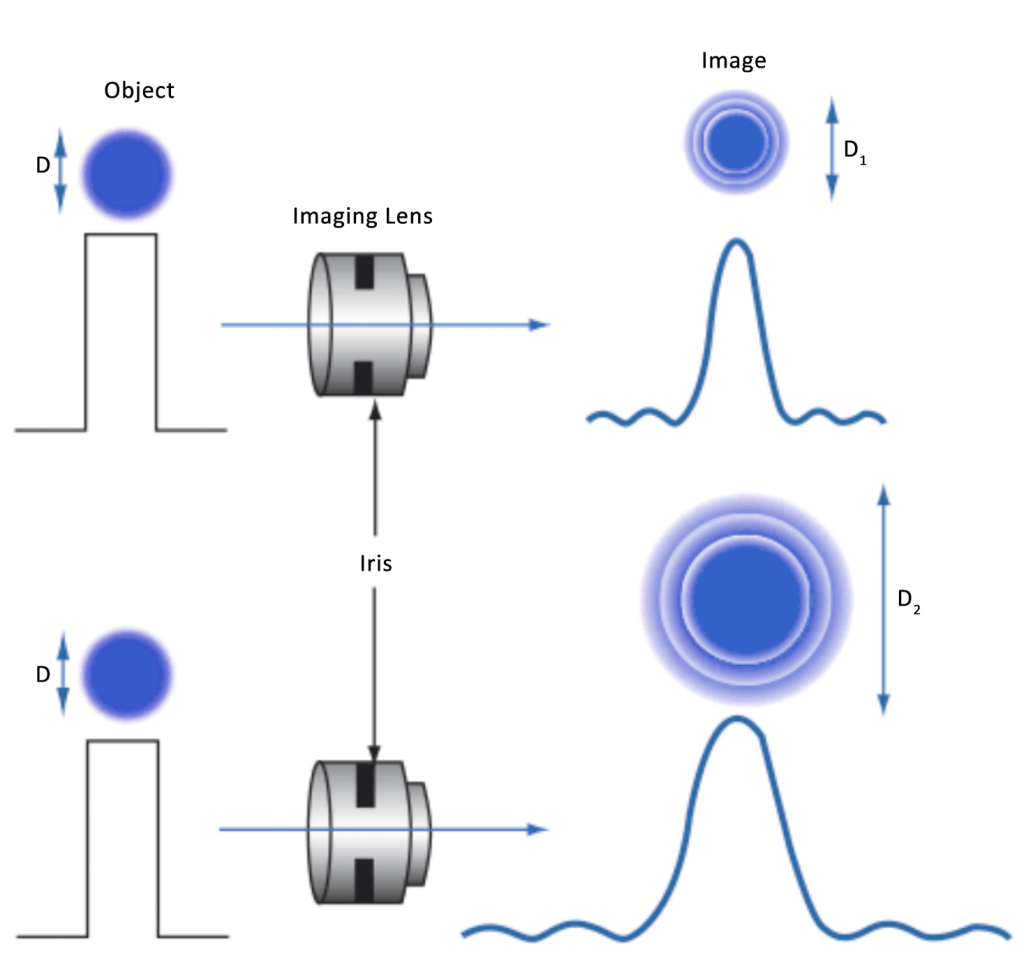
Figure 1 shows the difference in spot size between a lens set at f/2.8 and a lens set at f/8.
As the pixel size continues to decrease, its effect becomes more pronounced and eventually difficult to overcome. The Airy disk (or minimum spot size) can be calculated using f/# and wavelength (μm):
Minimum spot size (Airy disk diameter) [μm]=2.44⋅λ[μm]⋅f/#
An Airy Disc is a focused spot of light formed by a circular aperture in a diffraction-limited system. As shown in Figure 2, it appears as a central bright spot surrounded by alternate light and dark Airy patterns.
The diffraction pattern is determined by the wavelength of the light and the size of the aperture through which the light passes. The central point of the Airy disk contains about 84% of the light intensity, and the remaining 16% is distributed in the diffraction pattern around this point.
Of course, when viewed with a microscope there will be many points of light on the specimen, so it is more appropriate to think in terms of a large number of Airy patterns rather than a single point of light as described by the “Airy disk”.
The three-dimensional representation of the Airy pattern shown on the right in Figure 2 is also known as the ‘point spread function’.

Abbe diffraction limit
In 1873, German physicist Abbe discovered the formula for the resolution limit of the microscope, which is called the Abbe limit. It is approximately equal to half the wavelength of light. The wavelength of violet light with the shortest wavelength in visible light is about 400 nanometers, and the Abbe limit is about 200 nanometers.
That is to say, if the distance between two points reaches 200 nanometers, the nanometer cannot be distinguished with an optical microscope. This is roughly equivalent to 1500x magnification. This is the resolution limit of the optical microscope.
The microscope also uses a convex lens, and the light passing through it will also produce an Airy disk. A point we see through the microscope is actually a spot of light. If the two observed points are relatively far apart, we can still distinguish them.
But if two points are so close that the Airy disks generated by them overlap, we won’t be able to distinguish between two points, but just see a blur. Therefore, the Airy disk also determines the resolution limit of the microscope.
Formula: δ=0.61λ/(nSinα),
δ: Resolution λ: Wavelength n: Refractive Index α: Aperture Angle
Rayleigh Criterion
Rayleigh Criterion refers to the imaging optical system, the resolution is to measure the ability to separate the images of two adjacent object points.
Due to diffraction, the image formed by the system is no longer an ideal geometric point image, but a light spot (Airy disk) of a certain size. When two object points are too close and their image spots overlap, they may not be able to distinguish It is the image of two object points, that is, there is a resolution limit in the optical system, and this resolution limit usually adopts the criterion proposed by Rayleigh: when the center of one Airy disk coincides with the first-order dark ring of another Airy disk At this time, two images can just be distinguished.
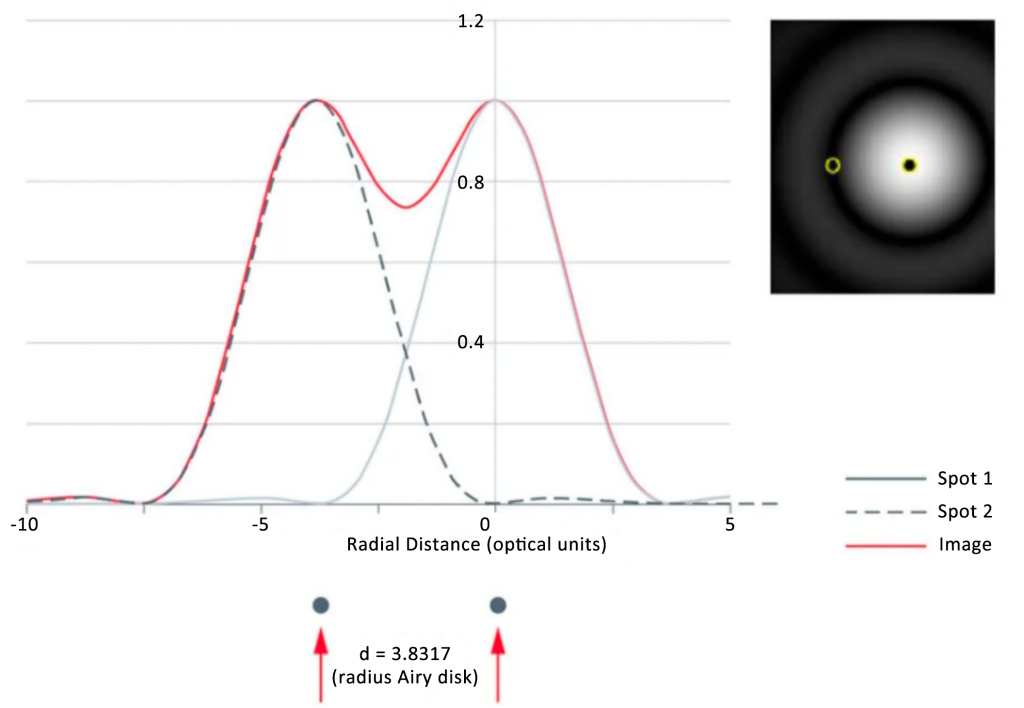
Using the Airy disk theory, if the diffraction patterns of 2 separate Airy disks do not overlap, then the two can be easily distinguished, ‘distinguished’ and deemed to satisfy the Rayleigh criterion (Figure 3, left panel). When the center of the Airy disk directly overlaps with the first minimum diffraction pattern of another Airy disk, the two are regarded as ‘just resolved’, and can still be distinguished as two independent light spots (Fig. 3, middle panel ). If the Airy discs continue to approach each other, the two do not satisfy the Rayleigh criterion and are therefore “indistinguishable” as 2 distinct points of light (or separate details in the image of the specimen; Figure 3, right panel).
How to Calculate the Resolution of a Microscope
Taking all of the above theories into account, it becomes apparent that there are many factors to consider when calculating the theoretical limit of resolution. The resolution also depends on sample properties. Let’s look at resolution calculations using Abbe’s diffraction limit and using Rayleigh’s criterion.
First of all, you should keep in mind:
NA= n x sin α
In the formula, n is the refractive index of the imaging medium, and α is half of the aperture angle of the objective lens. The maximum aperture angle of the objective lens is approximately 144º. The sine of half of this angle is 0.95. If an oil immersion objective is used with a refractive index of 1.52, the maximum NA of the objective is 1.45. If a ‘dry’ (no immersion) objective is used, the maximum NA of the objective is 0.95 (because air has a refractive index of 1.0).
The Abbe diffraction formula for lateral (i.e. XY) resolution is:
d = λ/2 NA
where λ is the wavelength of light used for imaging the specimen. If you use green light at 514 nm and an oil immersion objective with an NA of 1.45, the (theoretical) limit of resolution is 177 nm.
The Abbe diffraction formula for axial (i.e. Z) resolution is:
d= 2λ/NA2
Likewise, if we assume that the specimen is viewed through light with a wavelength of 514 nm and the objective lens has an NA of 1.45, then the axial resolution is 488 nm.
On the basis of Abbe’s diffraction limit, the Rayleigh criterion has been slightly refined:
R= 1.22 λ/NAobj+NAcond
where λ is the wavelength of light used for imaging the specimen. NAobj is the objective lens NA. NAcond is the condenser lens NA. ‘1.22’ is a constant coefficient. This value is derived from Rayleigh’s research on Bessel functions. These are mainly used to perform calculations on problems in the system, such as wave propagation.
Taking the NA of the condenser into account, air (refractive index 1.0) is usually the imaging medium between the condenser and the slide. Assuming the condenser has an aperture angle of 144º, the NAcond value will be equal to 0.95.
If you use green light at 514 nm, with an NA of 1.45 for the oil immersion objective and 0.95 for the condenser, the (theoretical) limit of resolution would be 261 nm.
As mentioned above, the shorter the wavelength of light used to image the specimen, the more detail can be resolved. So if the shortest visible wavelength of 400 nm is used, the NA of the oil immersion objective is 1.45, and the NA of the condenser is 0.95, then R equals 203 nm.
To achieve maximum (theoretical) resolution in a microscope system, each optical component should have the highest available NA (taking aperture angle into account). In addition, the shorter the wavelength of light used to view the specimen, the better the resolution. Finally, the entire microscope system should be collimated.
